Trabajo 4: Muestra de los conceptos de medias estadisticas y sus aplicaciones
MEDIA ARITMETICA
En matemáticas y estadística, la media aritmética, también llamada promedio o media, de un conjunto finito de números es el valor característico de una serie de datos cuantitativos, objeto de estudio que parte del principio de la esperanza matemática o valor esperado, se obtiene a partir de la suma de todos sus valores dividida entre el número de sumandos. Cuando el conjunto es una muestra aleatoria recibe el nombre de media muestral siendo uno de los principales estadísticos muestrales.
Formula general
.png)
PROPIEDADES
-
La suma de las desviaciones con respecto a la media aritmética es cero (0).
-
La media aritmética de los cuadrados de las desviaciones de los valores de la variable con respecto a una constante cualquiera se hace mínima cuando dicha constante coincide con la media aritmética.
-
Si a todos los valores de la variable se le suma una misma cantidad, la media aritmética queda aumentada en dicha cantidad.
-
Si todos los valores de la variable se multiplican por una misma constante la media aritmética queda multiplicada por dicha constante.
-
La media aritmética de un conjunto de números positivos siempre es igual o superior a la media geométrica.
Ejemplo 1:
En un test realizado a un grupo de 42 personas se han obtenido las puntuaciones que muestra la tabla. Calcula la puntuación media.
.png)
En primer lugar vamos a calcular la sumatoria de xi · fi, crearemos una nueva columna para los productos de la variable por su frecuencia absoluta y lo sumaremos todo
También tenemos que calcular N que es la sumatoria de las frecuencias absolutas
.png)
Media aritmetica
.png)
Ejemplo 2:
Los pesos de seis amigos son: 84, 91, 72, 68, 87 y 78 kg. Hallar el peso medio.
.png)
MEDIA PONDERADA
La media ponderada es una medida de tendencia central, que es apropiada cuando en un conjunto de datos cada uno de ellos tiene una importancia relativa (o peso) respecto de los demás datos. Se obtiene multiplicando cada uno de los datos por su ponderación (peso) para luego sumarlos, obteniendo así una suma ponderada; después se divide esta entre la suma de los pesos, dando como resultado la media ponderada.
Formula general
.png)
Ejemplo 1:
Cálculo de la nota de una asignatura donde el examen final tiene un peso mayor que un trabajo.
.png)
Se hace la media ponderada que es la suma de los productos de las notas por el peso de cada nota y se divide por la suma de los pesos.
.png)
Ejemplo 2:
Se puede usar una media ponderada para calcular la nota final de un curso escolar, en donde se asigna distinta importancia (peso) a los distintos exámenes que se realicen. Por ejemplo, los dos primeros exámenes tienen un peso o valor de 30% y 20% respectivamente, y el último del 50%; las calificaciones respectivas son de 6.4, 9.2 y 8.1, entonces la nota final corresponde a la siguiente media ponderada:
.png)
MEDIA GEOMETRICA
En matemáticas y estadística, la media geométrica de una cantidad arbitraria de números (por decir n números) es la raíz n-ésima del producto de todos los números; es recomendada para datos de progresión geométrica, para promediar razones, interés compuesto y números índices.
Formula general
.png)
Ejemplo 1:
En una empresa quieren saber la proporción media de mujeres en los diferentes departamentos. Para ello, se recoge el porcentaje de mujeres en los cinco principales departamentos.

Como es la media de porcentajes, calculamos la media geométrica que es más representativa.
Ejemplo 2:
Hallar la media geometrica de las 3 notas (01,03,09)de un estudiante de ingenieria electronica de la facultad FIMEE,que corresponden a sus tres practicas en el curso de Dibujo de Ingenieria.
.png)
MEDIA ARMONICA
La media armónica (designada usualmente mediante H) de una cantidad finita de números es igual al recíproco, o inverso, de la media aritmética de los recíprocos de dichos valores y es recomendada para promediar velocidades.
Formula general
.png)
Ejemplo 1 :
Supongase que una familia realiza un viaje en automóvil a un ciudad y cubre los primeros 100 km a 60 km/h, los siguientes 100 km a 70 km/h y los últimos 100 km a 80 km/h. Calcular, en esas condiciones, la velocidad media realizada.
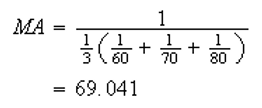
Ejemplo 2:
Un tren realiza un trayecto de 400km. La vía tiene en mal estado que no permitían correr. Los primeros 100 km los recorre a 120km/h, los siguientes 100km la vía está en mal estado y va a 20km/h, los terceros a 100km/h y los 100 últimos a 130km/h. Para calcular el promedio de velocidades, calculamos la media armónica.

MEDIA ARITMETICO-GEOMETRICA
La media aritmético-geométrica M(x, y) de dos números reales positivos x e y se define de la siguiente forma:
-
Primero, se obtiene la media aritmética de x e y denominándola a1, i.e. a1 = (x+y) / 2.
-
Después se calcula la media geométrica de x e y denominándola g1, i.e. g1 es la raíz cuadrada de xy.
-
A continuación, se itera esta operación con a1 en lugar de x y g1 en lugar de y. De esta forma, se definen dos sucesiones (an) y (gn):
.png)
Se demuestra que :
.png)
Ejemplo 1:
Hallar la media aritmetico-geometrica de los numeros 7 y 13:
.png)
Ejemplo 2:
Hallar la media aritmetico-geometrica de los numeros 8 y 12:
.png)


